SOAL EKSPONEN DAN PENYELESAIANNYA

SOAL EKSPONEN DAN PENYELESAIANNYA

1. Jika mtk1-10, maka mtk2-10= ....

mtk3-2

Kunci : A

Pembahasan:

mtk4-1 

2. Jikamtk5-1, maka mtk6-1= ....

mtk7-1

Kunci : A

Pembahasan:

Kuadratkan kedua ruas persamaan mtk5-1, sehingga:

mtk8-1

maka

mtk9-1


3. 3. Nilai x yang memenuhi persamaan mtk10-1adalah ....

mtk11-1

Kunci : B

Pembahasan:

mtk12-1


4.  Nilai dari mtk27-1= ....

  1.   10
  2.   9
  3.   8
  4.   7
  5.   6

Kunci : D

Pembahasan :

mtk28

Dengan cara yang sama diperoleh :

mtk29-1

Sehingga diperoleh :

mtk30

5.Bentuk sederhana dari  = ...

Pembahasan:


Jawaban: E

6.  Bentuk sederhana dari adalah ...
a.    22 - 24√3
b.    34 - 22√3
c.    22 + 34√6
d.    34 + 22√6
e.    146 + 22√6
Pembahasan:

= 30.3 - 20√6+42√6-28.2
= 90 + 22√6 – 56
= 34 + 22√6
Jawaban: D


7.Bentuk sederhana dari ( 1 + 3√2) – ( 4 – √50 ) adalah ….

A. – 2√2 – 3  

B. – 2√2 + 5

C. 8 √2 – 3     

D. 8 √2 + 3  

E. 8 √2 + 5

Jawaban : C

Pembahasan : 

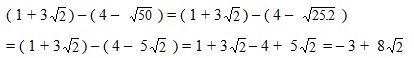
soal eksponen no 7

8. √75 + 2√12 - √27 = . . . . .

A. 2√3    
B. 3√3    
C. 4√3    
D. 5√3    
E. 6√3
Pembahasan:
√75 + 2√12 - √27 = √(25x3) + 2√(4x3) - √(9x3)
                               = (√25 x √3) + 2 x (√4 x √3) - (√9 x √3)
                               = 5√3 + 4√4 - 3√3
                               = (5+4-3)√3
                               = 6√3  -------> Jawaban: E

9. (√7 + √2)(√7 - √2) = . . . . ..
A. 2    
B. 5    
C. 7    
D. 2√7    
E. 2√2
Pembahasan:
(√7 + √2)(√7 - √2) = √7.√7 - √7.√2 + √7.√2 - √2.√2
                                 = 7 - √14 + √14 - 2
                                 = 7 - 0 - 2
                                 = 5 -----------> Jawaban: B 

10.  Jika a = (5 + √50), b = (2 + √18) dan c = (7 - √32) maka bentuk paling sederhana dari (a + b - c) adalah. . . . .
A. 6    
B. 2√2    
C. √2    
D. 4√2    
E. 12√2
Pembahasan: E
a + b - c = (5 + √50) +  (2 + √18) - (7 - √32)
               = 5 + √50 + 2 + √18 - 7 + √32
               = 5 + 2 - 7 + √50 + √18 + √32
               = 0 + √(25x2) + √(9x2) + √(16x2)
               = (√25 x √2) + (√9 x √2) + (√16 x √2)
               = 5√2 + 3√2 + 4√2
               = 12√2

11. Bentuk  sama dengan . . . . .
A. 13(4 + √3)
B. 13(4 - √3)
C. 13/7 (4 + √3)
D. (4 + √3)
E. (4 - √3)
Pembahasan:
  =  x 
                = 
                = 
                = (4 + √3) -----> Jawaban: D

12. Jika penyebut pecahan  dirasionalkan, maka bentuknya ekuivalen dengan . . . .
A. 2√5 + √3
B. 2√5 + 2√3
C. 2√5 - √3
D. 2√5 - 2√3
E. 2√2
Pembahasan:
 =  x 
                    = 
                    = 2(√5 + √3)
                    = 2√5 + 2√3 ------> Jawaban: B

13. Dengan merasionalkan penyebut dari  , bentuk sederhananya adalah...
A. -7 - 4√3
B. -7 + 4√3
C. -1 + (4/7)√3
D. 1 - (4/7)√3
E. 1 + 4√3
Pembahasan:
 =  x 
                = 
                = 
                = -7 + 4√3 ----> Jawaban: B

14. Penyelesaian persamaan \sqrt{3^{2x+1}} = 9^{x-2}

A. 0

B. 1\frac{1}{2}

C. 2

D. 3\frac{1}{2}

E. 4\frac{1}{2}

PEMBAHASAN :

\sqrt{3^{2x+1}} = 9^{x-2}

(32x + 1)1/2 = 32(x – 2)

3x + 1/2 = 32x – 4

x + \frac{1}{2} = 2x – 4

x = \frac{9}{2}

JAWABAN : E


15. Jika n bilangan bulat, maka nilai dari \frac{2^{n+2}.6^{n-4}}{12^{n-1}}  = …

A. \frac{1}{27}

B. \frac{1}{16}

C. \frac{1}{9}

D. \frac{1}{8}

E. \frac{1}{3}

PEMBAHASAN :

\frac{2^{n+2}.6^{n-4}}{12^{n-1}}  = \frac{2^{n+2}.6^{n-4}}{(2.6)^{n-1}}

= \frac{2^{n+2}.6^{n-4}}{2^{n-1}.6^{n-1}}

= 2n + 2 . 2-(n – 1) . 6n – 4 . 6-(n – 1)

= 2n + 2 . 2-n + 1 . 6n – 4 . 6-n + 1

= 23 . 6-3

= \frac{2.2.2}{6.6.6}

= \frac{1}{3.3.3}

= \frac{1}{27}

JAWABAN : A

Komentar

Posting Komentar

Postingan populer dari blog ini

VEKTOR, JENIS VEKTOR, OPERASI VEKTOR DAN CONTOH SOALNYA

Gambar
  VEKTOR, JENIS VEKTOR, OPERASI VEKTOR DAN CONTOH SOALNYA Vektor adalah sebuah besaran yang berarah.  Vektor juga bisa digambarkan sebagai panah yang menunjukan arah vektor dan panjang garisnya disebut juga Besar Vektor. Vektor yang berawal dari titik A dan berakhir di titik B bisa ditulis sebagai : atau Jenis – Jenis Vektor Vektor juga memiliki beberapa jenis tersendiri, yaitu sebagai berikut. 1. Vektor Posisi Vektor Posisi adalah vektor yang titik awalnya di titik 0 (0,0) dan titik ujungnya di A (a 1 , a 2 ).  2. Vektor 0 (Nol) Vektor 0 adalah vektor yang panjangnya nol dan dinotasikan Vektor nol tidak memiliki arah vektor yang jelas. 3. Vektor Satuan Vektor satuan adalah vektor yang panjangnya satu satuan. Vektor satuan dari  adalah Vektor di R 2 Panjang sebuah segmen garis yang menyatakan vektor  atau dinotasikan sebagai Panjang vektor sebagai : Panjang vektor tersebut ialah dapat dikaitkan dengan sudut θ yang dibentuk oleh vektor dan sum...
Baca selengkapnya