SOAL PERTIDAKSAMAAN EKSPONEN DAN SIFAT-SIFATNYA

 

SOAL PERTIDAKSAMAAN EKSPONEN DAN SIFAT-SIFATNYA

1. Nilai x yang memenuhi pertidaksamaan eksponen 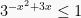 adalah:

Pembahasan

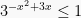
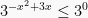
Sehingga,

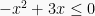
Diperoleh,

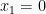 dan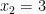 

Untuk mendapat penyelesaiannya, ambil sembarang nilai x diantara rentang  kemudian disubstitusikan kedalam bentuk 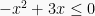. Misal ambil x = 1.

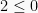 (tidak sesuai)

Karena tidak sesuai, maka area penyelesaian ada di luar rentang , sehingga didapat penyelesaiannya adalah

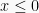 dan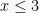 

2. Himpunan penyelesaian dari pertidaksamaan eksponen 

$\begin{array}{c}{9}^{2x-4}\ge {\left(\frac{1}{27}\right)}^{x^2-4}\end{array}$ adalah ...
A.   {x / -2 ≤ x ≤ 10/3}
B.   {x / -10/3 ≤ x ≤ 2}
C.   {x / x ≤ -10/3  atau  x ≥ 2}
D.   {x / x ≤ -2  atau  x ≥ 10/3}
E.   {x / -10/3 ≤ x ≤ -2}

Pembahasan :
$\begin{array}{cc}{9}^{2x-4}& \ge {\left(\frac{1}{27}\right)}^{x^2-4}\\ {\left(3^2\right)}^{2x-4}& \ge {\left(3^{-3}\right)}^{x^2-4}\\ 3^{2(2x-4)}& \ge 3^{-3(x^2-4)}\\ 2(2x-4)& \ge -3(x^2-4)\\ 4x-8& \ge -3x^2+12\\ 3x^2+4x-20& \ge 0\end{array}$

Pembuat nol :
3x² + 4x - 20 = 0
(3x + 10)(x - 2) = 0
x = -10/3  atau  x = 2

Dengan uji garis bilangan diperoleh
x ≤ -10/3  atau  x ≥ 2

Jawaban : C

3. Nilai x yang memenuhi pertidaksamaan 5^2x - 6.5^x+1 + 125 > 0, x ∈ R adalah ...

A.   1 < x < 2
B.   5 < x < 25
C.   x < -1  atau  x > 2
D.   x < 1  atau  x > 2
E.   x < 5  atau  x > 25

Pembahasan :
5^2x  -  6.5^x+1  +  125  >  0
(5^x)²  -  6.5^x.5¹  +  125  >  0
(5^x)²  -  30(5^x)  +  125  >  0

Misalkan y = 5^x, pertidaksamaan diatas menjadi
y² - 30y + 125 > 0

Pembuat nol :
y² - 30y + 125 = 0
(y - 5)(y - 25) = 0
y = 5  atau  y = 25

Dengan uji garis bilangan diperoleh
y < 5  atau  y > 25

Karena y = 5^x, maka penyelesaiannya menjadi
5^x < 5  atau  5^x > 25
5^x < 5¹  atau  5^x > 5²
x < 1  atau  x > 2

Jawaban : D

4. Nilai x yang memenuhi pertidaksamaan 3.4^x - 7.2^x + 2 > 0 adalah ...

A.   x < -1  atau x > ²log 3
B.   x < ²log 1/3  atau  x > 1
C.   ²log 1/3 < x < 1
D.   x < 1  atau  x > ²log 1/3
E.   1 < x < ²log 1/3

Pembahasan :
3.4^x  -  7.2^x  +  2  >  0
3(2^x)²  -  7(2^x)  +  2  >  0

Misalkan y = 2^x, pertidaksamaan diatas menjadi
3y² - 7y + 2 > 0

Pembuat nol :
3y²  - 7y + 2 = 0
(3y - 1)(y - 2) = 0
y = 1/3  atau  y = 2

Dengan uji garis bilangan diperoleh
y < 1/3  atau  y > 2

Karena y = 2^x, maka
2^x < 1/3             atau  2^x > 2
$2^x$ < $2^{{}^{2}log1/3}$  atau  2^x > 2¹
x < ²log 1/3   atau  x > 1

Jadi, nilai x yang memenuhi adalah
x < ²log 1/3  atau  x > 1

Jawaban : B

5. Tentukan himpunan penyelesaian dari pertidaksamaan eksponen 49^3x-4 > 7^x2!

Pembahasan:

Untuk menentukan solusinya, Quipperian harus menyamakan basis pada kedua ruas. Berdasarkan sifat-sifat eksponen diperoleh:

Oleh karena a = 7 > 1, maka berlaku:

Titik pembuat nol x = 4 dan x = 2.

6. 

karena bilangan pokok a=2 >0 maka

2x-5 > 16-5x

7x > 21

x> 3 jadi solusi dari persamaan (*) adalah x>3

7. 

perhatikan,tanda pertidaksamaan dibalik karena bilangan pokoknya dalam bentuk pecahan atau 0< a<1,sehingga

2x-5 < 16-5x

21 > 7x

3> x jadi solusi dari persamaan (*) adalah x<3

8. Hasil produksi suatu barang dinyatakan dengan persamaan P(x) = –x2 +28x – 60 unit barang untuk bahan baku yang diperlukan. Apabila hasil produksi (P) mencapai lebih dari 100 unit, maka banyaknya bahan baku x yang diperlukan adalah…

Jawab

■ Hasil produksi mencapai lebih dari 100 unit berarti P(x) > 100 sehingga

⇔ –x2 +28x – 60 > 100

⇔ –x2 +28x – 60 – 100 > 0

⇔ –x2 +28x – 160 > 0

⇔ x2 – 28x + 160 < 0

⇔ (x – 20)(x – 8) < 0

Dari sini kita peroleh x = 8 dan x = 20

■ Kita tentukan batas interval yang memenuhi pertidaksamaan x2 – 28x + 160 < 0 yaitu sebagai berikut.

Tabel Hasil Uji Interval

Nilai Uji	Nilai x2 – 28x + 160 = 0	Tanda Interval
x = 0 (x < 8)	(0)2 – 28(0) + 160 = +160	+ atau > 0
x = 9 (8 < x < 20)	(9)2 – 28(9) + 160 = –11	− atau < 0
x = 21 (x > 20)	(21)2 – 28(21) + 160 = +43	+ atau > 0

■ Dari tabel hasil uji interval di atas, maka interval yang memenuhi pertidaksamaan x2 – 28x + 160 < 0 adalah 8 < x < 20.

■ Dengan demikian, banyaknya bahan baku yang dibutuhkan adalah lebih dari 8 unit dan kurang dari 20 unit.

9. Sebuah peluru ditembakkan ke atas. ketinggian peluru yang dicapai (dalam meter) dinyatakan sebagai h(t) = 30t – t2. Berapa lamakah peluru itu berada pada ketinggian tidak kurang dari 221 meter?

Jawab

■ Ketinggian peluru tidak kurang dari 221 meter, berarti h(t) ≥ 221 sehingga

⇔ 30t – t2 ≥ 221

⇔ 30t – t2 – 221 ≥ 0

⇔ t2 – 30t + 221 ≤ 0

⇔ (t – 13)(t – 17) ≤ 0

Sampai sini kita dapatkan t = 13 dan t = 17

■ Kita tentukan batas interval yang memenuhi pertidaksamaan t2 – 30t + 221 ≤ 0 yaitu sebagai berikut.

Tabel Hasil Uji Interval

Nilai Uji	Nilai t2 – 30t + 221 = 0	Tanda Interval
t = 0 (t < 13)	(0)2 – 30(0) + 221 = +221	+ atau > 0
t = 14 (13 < t < 17)	(14)2 – 30(14) + 221 = –3	− atau < 0
t = 18 (x >17)	(18)2 – 30(18) + 221 = +5	+ atau > 0

■ Dari tabel hasil uji interval di atas, maka interval yang memenuhi pertidaksamaan t2 – 30t + 221 ≤ 0 adalah 13 ≤ t ≤ 17.

■ Dengan demikian, peluru akan berada pada ketinggian tidak kurang dari 221 meter yaitu dari detik ke-13 sampai dengan detik ke-17 atau dalam selang waktu (17 – 13) detik = 4 detik.

10. Keliling sebuah persegi panjang sama dengan 20 cm. Jika luas persegi panjang itu tidak kurang dari 21 cm2, maka tentukanlah batas-batas nilai panjang dari persegi panjang tersebut.

Jawab

■ Misalkan panjang dan lebar persegi panjang tersebut adalah x cm dan y cm. Maka keliling persegi panjang adalah K = 2(x + y) = 20

⇔ 2(x + y) = 20

⇔ x + y = 10

⇔ y = 10 – x

Luas persegi panjang adalah adalah L = x . y

⇔ L = x(10 – x)

⇔ L = 10x – x2

■ Dari soal telah ditentukan bahwa luas persegi panjang tidak kurang dari 21 cm2, hal ini berarti L ≥ 21 sehingga

⇔ 10x – x2 ≥ 21

⇔ 10x – x2 – 21 ≥ 0 (kita ubah –x2 menjadi x2 dengan mengali kedua ruas dengan -1)

⇔ x2 – 10x + 21 ≤ 0 (jika kedua ruas dikali dengan bilangan negatif, maka tanda berubah)

⇔ (x – 3)(x – 7) ≤ 0

Dari sini kita peroleh x = 3 dan x = 7

■ Kita tentukan batas interval yang memenuhi pertidaksamaan x2 – 10x + 21 ≤ 0 yaitu sebagai berikut.

Tabel Hasil Uji Interval

Nilai Uji	Nilai x2 – 10x + 21 = 0	Tanda Interval
x = 0 (x < 3)	(0)2 – 10(0) + 21 = +21	+ atau > 0
x = 4 (3 < x < 7)	(4)2 – 10(4) + 21 = –3	− atau < 0
x = 8 (x > 7)	(8)2 – 10(8) + 21 = +5	+ atau > 0

■ Dari tabel hasil uji interval di atas, maka interval yang memenuhi pertidaksamaan x2 – 10x + 21 ≤ 0 adalah 3 ≤ x ≤ 7.

■ Dengan demikian, batas-batas nilai panjang dari persegi panjang itu adalah mulai dari 3 cm sampai dengan 7 cm.