PERTIDAKSAMAAN EKSPONEN DAN SIFAT-SIFATNYA
PERTIDAKSAMAAN EKSPONEN DAN SIFAT-SIPATNYA
Pertidaksamaan eksponen adalah pertidaksamaan jenis eksponen yang memiliki variabel.

Untuk menentukan solusi pertidaksamaan eksponen seperti pertidaksamaan di atas, ikuti langkah berikut.
- Bentuk eksponen harus diuraikan sampai diperoleh bentuk yang sama. Uraikan berdasarkan sifat-sifat eksponen.
- Gunakan permisalan bentuk eksponen dengan variabel tertentu.
- Selesaikan pertidaksamaannya menggunakan konsep pertidaksamaan sampai diperoleh interval untuk permisalannya.
- Susbtitusikan nilai balik yang diperoleh pada permisalan.
Dalam bentuk pertidaksamaan, sifat-sifat pertidaksamaan eksponen dapat diketahui sebagai berikut:
Untuk 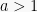
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
Untuk 
Jika , maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
- Jika
, maka
Contoh:
Maka:
Komentar
Posting Komentar