SOAL PERSAMAAN LOGARITMA DAN SIFAT-SIFATNYA

 

SOAL PERSAMAAN LOGARITMA DAN SIFAT-SIFATNYA

1. Nilai dari 2log 4 + 2log 12 – 2log 6 =…

---

1. 8
2. 6
3. 5
4. 4
5. 3

---

Pembahasan :

Untuk soal seperti di atas, maka kita perlu mengingat sifat logaritma

alog(b.c) = alog b + alog c, dan

alog  = alog b – alog c

sehingga, untuk menyelesaikan soal di atas, kita gunakan kedua sifat logaritma tersebut. Dimana perhitungannya akan menjadi :

2log 4 + 2log 12 – 2log 6           = 2log

                                    = 2log 8

Kemudian, untuk penyelesaian akhir, kita perlu mengingat sifat berikutnya, yaitu :

alog  = n .  alog b

→ 8 =

sehingga, penyelesaian akhirnya akan menjadi seperti berikut ini :

2log 8   = 2log

            = 3 . 2log 2       → jangan lupa dengan yang ini : alog a = 1

            = 3 . 1

            = 3       ( E )

2. Nilai dari 2log 48 + 5log 50 – 2log 3 – 5log 2 =…

---

1. -2
2. -6
4. 2
5. 6

---

Pembahasan :

Sebelum mengerjakan, mari kita lihat perbedaan antara soal no. 1 dengan no. 2. Perbedaannya adalah :

• Pada soal no. 1, indeks logaritma merupakan indeks yang seragam ( indeks 2 )
• Sedangkan pada soal no. 2, indeks logaritma yang digunakan indeks tidak seragam ( indeks 2 dan indeks 5 )

---

Nah, tentu saja dengan perbedaan seperti ini, maka kita tidak bisa langsung menyelesaikannya seperti soal no. 1 di atas. Akan tetapi, soal no. 2 ini perlu di utak-atik sedikit supaya bisa diselesaikan dengan sifat-sifat yang ada.

---

Utak-atik yang perlu kita lakukan adalah dengan menggabungkan masing-masing logaritma dengan yang sejenis atau ber-indeks sama ( indeks 2 dengan indeks 2, indeks 5 dengan indeks 5 ), sehingga soal tersebut akan menjadi :

---

2log 48 – 2log 3 + 5log 50 – 5log 2  =…

Kemudian, soal tersebut bisa kita hitung dengan sifat :

---

alog  = alog b – alog c

2log 48 – 2log 3 + 5log 50 – 5log 2 = 2log  + 5log

                                                                          = 2log 16 + 5log 25

---

Sekarang kita gunakan sifat berikutnya : alog  = n .  alog b

→ 16 =

→ 25 =

Dan juga gunakan sifat : alog a = 1

Sehingga, penyelesaiannya akan menjadi :

2log    + 5log  = 4 . 2log  + 2 . 5log

                                       = 4 + 2

                                       = 6    ( E )

3. Tentukan penyelesaian dari 

Pembahasan :

4. Tentukan nilai x dari persamaan   (UMPTN ’93)

Pembahasan :

Misalkan , maka persamaannya:

Akarnya adalah ,namun  tidak bisa jadi penyelesaian karena bernilai negatif.

Sehingga:

Jika 

5. Carilah himpunan penyelesaian dari ²log(x² + 4x) = 5

Pembahasan

²log(x² + 4x) = 5
²log(x² + 4x) = ²log 2^5
2log(x² + 4x) = ²log 32

maka :
x² + 4x = 32
x² + 4x - 32 = 0
(x - 4)(x + 8) =
x = 4 dan x = -8

Himpunan penyelesaiannya adalah {-8, 4}

6. Carilah himpunan penyelesaian dari ⁵log(2x² + 5x - 10) = ⁵log(x² - 2x + 18)

Pembahasan

⁵log(2x² + 5x - 10) = ⁵log(x² - 2x + 18)
2x² + 5x - 10 = x² - 2x + 18
2x² - x² + 5x - 2x - 10 - 18 = 0
x² + 3x - 28 = 0
(x - 4)(x + 7) = 0
x=4 dan x=-7

Himpunan penyelesaiannya adalah {4,-7}

7. Carilah himpunan penyelesaian dari ⁴log(3x - 1) = ⁵log(2x + 2)

Pembahasan

⁴log(3x - 1) = ⁵log(2x + 2)
3x - 1 = 2x + 2
3x - 2x - 1 - 2 = 0
x - 3 = 0
x = 3

Himpunan penyelesaiannya adalah {3}

8. Tentukan nilai x dari persamaan logaritma ³log²x - 7.³log x + 12 = 0

Pembahasan

Misalkan : p = ³log x

Maka :
p² - 7p + 12 =
(p - 4)(p - 3) = p = 4 dan p = 3

Substitusi nilai p = ³log x, sehingga diperoleh nilai x:
³log x = p (masukkan nilai p = 4)
³log x = 4 ⇒ x = 3⁴ = 81

³log x = p (masukkan nilai p = 3)
³log x = 3 ⇒ x = 3³ = 27

Jadi nilai x nya adalah {81, 27}

9. Nilai x yang memenuhi persamaan 

${}^{2}log{}^{2}log\left(2^{x+1}+3\right)=1+{}^{2}logx$ adalah...
A.  ²log 3
B.  ³log 2
C.  log$\frac{2}{3}$
D.  −1 atau 3
E.  8 atau $\frac{1}{2}$

Pembahasan :
²log ²log(2^x+1 + 3) = 1 + ²log x

Syarat logaritma :
* 2^x+1 + 3 > 0 → x ∈ R
* ²log(2^x+1 + 3) > 0  → x ∈ R
* x > 0

Penyelesaian persamaan logaritma :
²log ²log(2^x+1 + 3) = 1 + ²log x
²log ²log(2^x+1 + 3) = ²log 2 + ²log x
²log ²log(2^x+1 + 3) = ²log 2x
²log(2^x+1 + 3) = 2x
2^2x = 2^x+1 + 3
 2^2x − 2^x+1 − 3 = 0
 (2^x)² − 2^x.2¹ − 3 = 0

Misalkan 2^x = y
 y² − 2y − 3 = 0
(y + 1)(y − 3) = 0
y = −1 atau y = 3

2^x = −1 → x ∉ R
2^x = 3 ⇔ x = ²log 3

Jawaban : A

10. Akar-akar dari persamaan 

${}^{2}lo{g}^{2}x-6{}^{2}logx+8={}^{2}log1$ adalah x₁ dan x₂. Nilai x₁ + x₂ =...
A.  6
B.  8
C.  10
D.  12
E.  20

Pembahasan :
²log²x − 6 ²log x + 8 = ²log 1

Syarat logaritma :
x > 0 ..............................(1)

Penyelesaian persamaan logaritma :
²log²x − 6 ²log x + 8 = ²log 1
(²log x)² − 6 ²log x + 8 = 0

Misalkan :  ²log x = y
y² − 6y + 8 = 0
(y − 2)(y − 4) = 0
y = 2 atau y = 4

²log x = 2 ⇔ x = 2² = 4
²log x = 4 ⇔ x = 2⁴ = 16

x₁ + x₂ = 4 + 16 = 20

Jawaban : E

11. Diketahui 

${}^{64}log\sqrt{{16}^{x-4}}=\frac{1}{2}$. Nilai x yang memenuhi persamaan tersebut adalah...
A.  −5$\frac{1}{2}$
B.  −4$\frac{3}{4}$
C.  4
D.  5$\frac{1}{2}$
E.  9$\frac{1}{2}$

Penyelesaian :
⁶⁴log$\sqrt{{16}^{x-4}}=\frac{1}{2}$

Syarat logaritma :
$\sqrt{{16}^{x-4}}$ > 0 → x ∈ R

Penyelesaian persamaan logaritma :
⁶⁴log$\sqrt{{16}^{x-4}}$ = $\frac{1}{2}$
⁶⁴log$\sqrt{{16}^{x-4}}$ = ⁶⁴log 64${}^{\frac{1}{2}}$
$\sqrt{{16}^{x-4}}$ = 64${}^{\frac{1}{2}}$  (kuadratkan kedua ruas)
16^x-4 = 64
2^4(x-4) = 2⁶
4(x − 4) = 6
4x − 16 = 6
4x = 22
x = 5$\frac{1}{2}$

Jawaban : D

12. Nilai x yang memenuhi persamaan 

${}^{\frac{1}{2}}log(x^2-3)-{}^{\frac{1}{2}}logx=-1$ adalah...
A.  x = −1 atau x = 3
B.  x = 1 atau x = −3
C.  x = 1 atau x = 3
D.  x = 1 saja
E.  x = 3 saja

Pembahasan :
${}^{\frac{1}{2}}$log(x² − 3) − ${}^{\frac{1}{2}}$log x = −1

Syarat logaritma :
* x² − 3 > 0
* x > 0

Penyelesaian persamaan logaritma :
${}^{\frac{1}{2}}$log(x² − 3) − ${}^{\frac{1}{2}}$log x = ${}^{\frac{1}{2}}$log ($\frac{1}{2}$)^-1
${}^{\frac{1}{2}}$log$\left(\frac{x^2-3}{x}\right)$ = ${}^{\frac{1}{2}}$log 2
$\frac{x^2-3}{x}$ = 2
x² − 3 = 2x
x² − 2x − 3 = 0
(x + 1)(x − 3) = 0
x = −1 atau x = 3

Berdasarkan syarat logaritma, maka yang memenuhi adalah x = 3

Jawaban : E

13. Tentukan hasil dari 3log81 – 3log8 + 3log72

pembahasan :

Untuk menyelesaikan soal ini, kita harus menggunakan sifat logaritma  log a x b = log a  + log b  dan alog a = 1. Pertama, pecah soal logaritma tersebut menjadi lebih kecil seperti penyelesaian di bawah ini.

=3log 81 – 3log 8 + 3log 72

=3log 34 – 3log 8 + 3log (9×8)  

=3log 34 – 3log 8 + 3log 32 + 3log 8

=3log 34 + 3log 32

=4+2 = 6

Setelah melalui penyederhanaan menggunakan sifat logaritma, hasil dari soal logaritma di atas adalah 6.

14. Diketahui jika 2log 5 = a dan 5log 3 = b. Maka nilai 15log 40

pembahasan :

Untuk menyelesaikan persoalan di atas, terdapat beberapa sifat logaritma yang perlu diperhatikan. Terdapat 4 sifat logaritma yang harus diterapkan dalam soal ini.

• alog b = log b / log a
• alog an = n
• log a x b = log a + log b
• alog b x blog c = alog c

Dalam mengerjakan soal tersebut, kita dapat menggunakan sifat logaritma keempat untuk mendapatkan hasil baru. Selanjutnya, menggunakan persamaan pertama, ketiga, dan kedua. Untuk lebih jelasnya, mari simak pembahasan soal logaritma berikut ini.

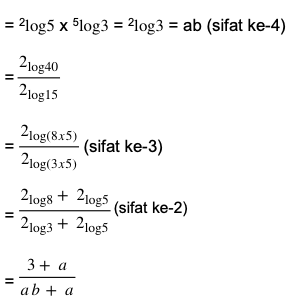
Penyelesaian soal logaritma di atas adalah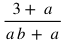 

15. Jika 8log 5 = 2a, maka 5log 64 adalah

pembahasan :

 Terdapat dua sifat logaritma yang bisa kamu gunakan untuk menyelesaikan soal tersebut yaitu alog bn = n alog b dan alog b = 1/ blog a . Langkah pertama yang dapat dilakukan adalah menggunakan sifat kedua logaritma di atas untuk menyelesaikan permasalahan ini seperti pembahasan di bawah ini.

Kita masukkan 2log 5 = 6a dengan menggunakan sifat kedua. Sehingga didapatkan persamaan logaritma seperti di bawah ini.

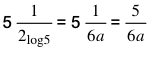
Sehingga hasil akhir dari 5log 64 adalah 5/6a