OPERASI VEKTOR DAN CONTOH SOALNYA

 

Operasi Vektor pada Bidang

Penjumlahan Vektor 

2 vektor atau lebih dapat dijumlahkan dan hasilnya dapat disebut resultan. 

Penjumlahan vektor secara aljabar dapat dilakukan dengan cara menjumlahkan komponen yang juga seletak. Jika

Maka

Secara grafis, penjumlahan vektor dapat dilihat pada gambar dibawah :

Sifat – sifat penjumlahan vektor adalah sebagai berikut.

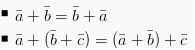
Pengurangan Vektor 

Dalam pengurangan vektor, berlaku sama dengan penjumlahan yaitu sebagai berikut:

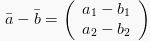
Perkalian Vektor dengan Skalar

Suatu vektor dapat dikalikan dengan suatu skalar (bilangan real) dan akan menghasilkan suatu vektor baru. 

Jika v adalah vektor dan k merupakan skalar. Maka perkalian vektor dapat dinotasikan:

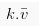
Keterangan:

Secara grafis perkalian ini dapat merubah panjang vektor. Lihat tabel berikut.

Perkalian vektor  dengan skalar k dapat dirumuskan sebagai berikut:

Perkalian Skalar 2 Vektor

Perkalian skalar dua vektor dapat disebut juga sebagai hasil kali titik dua vektor, ditulis sebagai berikut:

Contoh soal

1. Diketahui vektor a = 2 i - 3 j dan vektor b = -4 i - j , dan vektor c = - i + 2 j Tentukan vektor- vektor berikut nyatakan hasilnya dalam vektor - vektor basis i dan j :

a. a - b + c

b. a + 2 b - c

Jawab :

a. a - b + c = ( 2 i - 3 j ) - ( -4 i - j ) + ( - i + 2 j )

                  = ( 2 i + 4 i - i - 3 j + j + 2  j )

                  = - i

b. a + 2 b - c = ( 2 i - 3 j ) + 2 ( -4 i - j ) - ( - i + 2 j )

                     = ( 2 i - 3 j ) + ( - 8 i - 2 j ) - ( - i + 2 j )

                     = ( 2 i - 8 i + i - 3 j - 2 j - 2 j )

                     = 9 i - 3 j 

2. Diberikan 3 buah vektor: 

Bentuk sederhana dan perkaliannya dapat di lihat pada penyelesaian di bawah ini.